Physical Distancing
Kembali ke /editorial| Tingkat Kesulitan | Expert |
| Kategori | Ad Hoc, Advanced Data Structure |
| Pranala Soal | Pranala Soal |
| Pranala Solusi | Solusi $O(N^2)$, Solusi Penuh $O(Nd \log N)$ |
Untuk menyederhanakan, kita sebut dua orang “menabrak” jika mereka melanggar (atau akan melanggar) physical distancing.
Menentukan apakah dua orang menabrak
Sebut kedua orang ini $P_i$ dan $P_j$, dengan koordinat awal masing-masing $(x_i, y_i)$ dan $(x_j, y_j)$ dan kecepatan $v_i$ dan $v_j$. Pertama-tama, dua orang tidak akan menabrak jika jarak antara $x_i$ dan $x_j$ nya lebih dari $d$. Kita akan bagi menjadi dua kasus sesuai arah mereka, dengan anggapan bahwa $\vert x_i - x_j \vert \le d$.
-
Jika keduanya menghadap ke arah yang sama
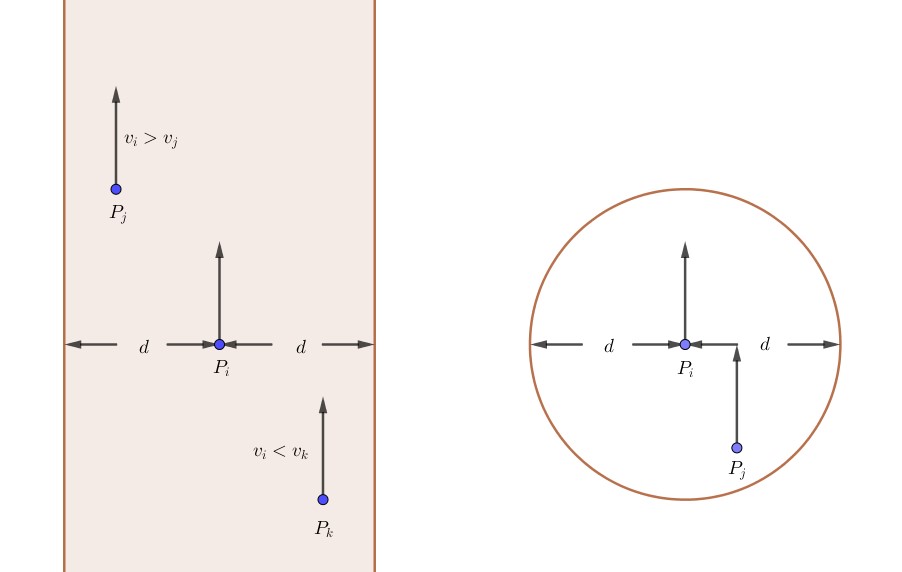
Misalkan keduanya berjalan ke utara ($v_i, v_j > 0$). Kita akan bagi menjadi dua kasus tergantung posisi $y_i$ dan $y_j$:
-
Jika $y_i \le y_j$, atau dengan kata lain posisi $P_i$ lebih selatan daripada posisi $P_j$.
Perhatikan bahwa pada kasus ini, $P_i$ akan “menyusul” $P_j$ (dengan kata lain, posisi $y$ nya akan sama) jika $v_i > v_j$.
Jika $v_i \le v_j$, jarak keduanya akan makin menjauh. Tapi ada kemungkinan kalau mereka sudah menabrak sejak awal, atau dengan kata lain, jika $distance((x_i, y_i), (x_j, y_j)) \le d$.
-
Jika $y_i > y_j$, atau dengan kata lain posisi $P_i$ lebih utara daripada posisi $P_j$.
Sama seperti subkasus sebelumnya, $P_i$ dan $P_j$ akan menabrak jika $v_j > v_i$ atau $distance((x_i, y_i), (x_j, y_j)) \le d$.
-
-
Jika keduanya berlawanan arah
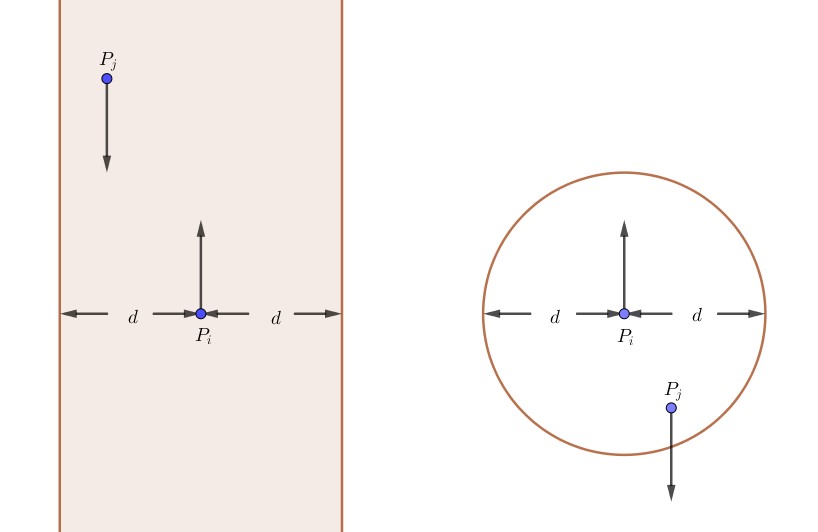
Kita bagi lagi menjadi dua kasus berdasarkan posisi $y_i$ dan $y_j$:
-
Jika $y_i \le y_j$, atau dengan kata lain posisi $P_i$ lebih selatan daripada posisi $P_j$.
Perhatikan bahwa tidak peduli kecepatan mereka berapa, suatu saat posisi $y$ keduanya akan sama. Jadi, dalam kasus ini, $P_i$ dan $P_j$ pasti akan menabrak.
-
Jika $y_i > y_j$, atau dengan kata lain posisi $P_i$ lebih utara daripada posisi $P_j$.
Sama seperti kasus yang arahnya sama, ada kemungkinan mereka menabrak di awal. Jadi, $P_i$ dan $P_j$ akan menabrak jika dan hanya jika jarak awalnya kurang atau sama dengan $d$, atau jika $distance((x_i, y_i), (x_j, y_j)) \le d$.
-
Menangani kasus $v = 0$
Kedua kasus di atas sudah mencakup semuanya, tapi kita harus hati-hati dalam memperhitungkan orang dengan kecepatan 0 (diam). Perhatikan bahwa argumen di atas tetap berlaku, jika kita meng-assign orang-orang dengan kecepatan 0 pada satu arah. Misalnya, anggap orang yang “bergerak ke utara” adalah orang-orang dengan kecepatan $v_i \ge 0$, dan orang yang “bergerak ke selatan” adalah orang-orang dengan kecepatan $v_i < 0$.
Solusi $O(N^2)$
Untuk 50% kasus, nilai $N$ cukup kecil untuk kita dapat membandingkan tiap pasang orang dan mengecek seluruh kasus di atas.
Solusi $O(Nd \log N)$
Perhatikan bahwa kita tidak mungkin membandingkan tiap pasang orang saat $N$ mencapai 100 ribu. Namun, perhatikan bahwa batasan $d$ cukup kecil, yaitu hanya $d \le 10$.
Kita dapat memproses orang-orang yang berlawanan arah dan yang berarah sama secara terpisah.
1. Menghitung pasangan orang yang berarah sama
Misalkan kita hanya memproses orang-orang yang bergerak ke utara ($v_i \ge 0$). Cara yang sama dapat dilakukan untuk orang-orang yang bergerak ke selatan ($v_i < 0$).
- Pertama, urutkan semua orang ini berdasarkan nilai $v_i$. Kita akan memproses orang mulai dari yang nilai $v_i$ nya paling kecil.
-
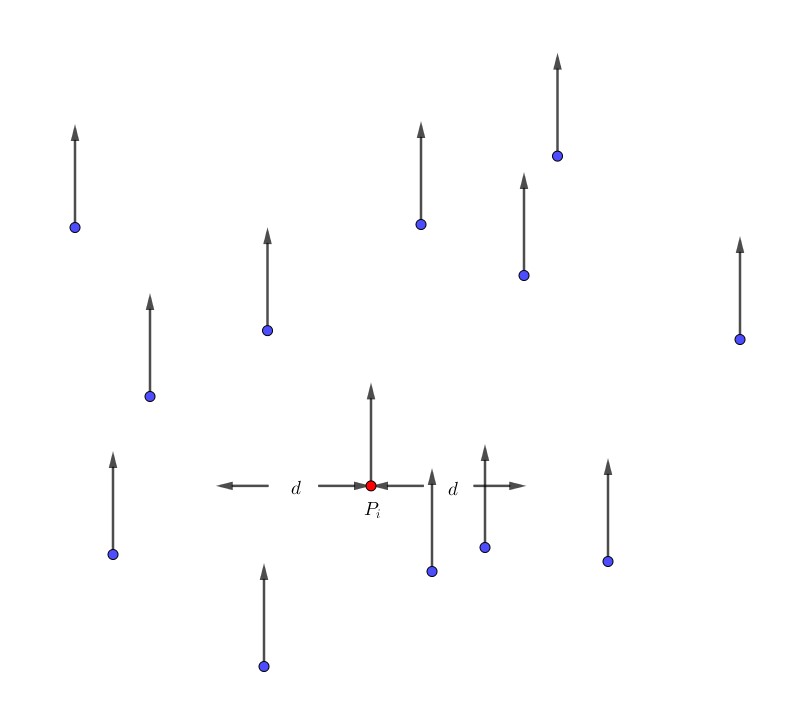
Misalkan kita akan memproses orang ke-$i$. Misalkan diagram berikut menunjukkan posisi orang ke-$i$, $d$, dan orang-orang yang sudah diproses sebelumnya.
-
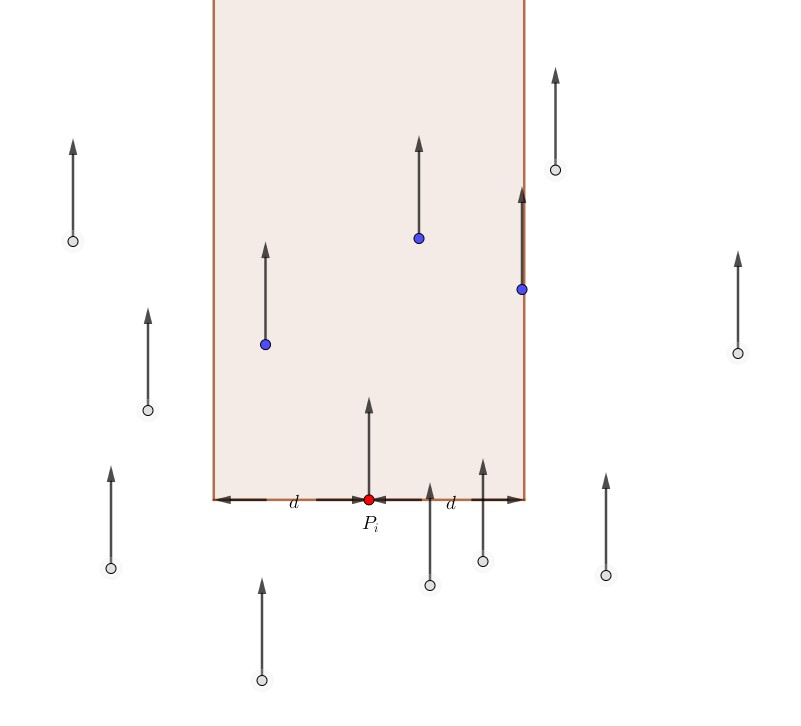
Pada subkasus 1.1 di atas, orang ke-$i$ ini akan menabrak orang-orang yang kecepatannya lebih rendah dan posisi $y$ nya lebih besar. Perhatikan bahwa kita telah memproses semua orang dengan kecepatan yang lebih rendah. Jadi, kita cukup mencari banyaknya orang yang telah diproses dengan selisih koordinat $x$ kurang atau sama dengan $d$, dan yang nilai $y$-nya $\ge y_i$. Berarti, kita harus mencari banyaknya orang di dalam persegi panjang berikut:
-
Pada subkasus 1.2 di atas, orang ke-$i$ ini akan menabrak orang-orang yang posisi $y$ nya lebih rendah dari $y_i$ dan jaraknya $\le d$. Berarti, kita harus mencari banyaknya orang pada setengah lingkaran berikut:
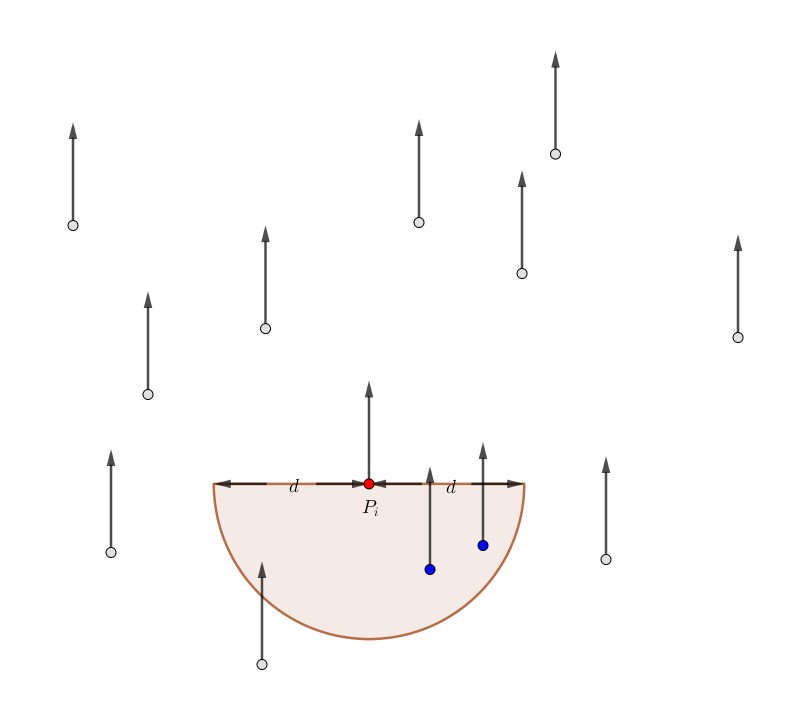
Perhatikan bahwa ada kemungkinan orang ke-$i$ ini akan berjarak $\le d$ dengan orang yang kecepatannya lebih besar, atau dengan kata lain dengan orang yang belum diproses saat kita memproses orang ke-$i$. Tapi, saat kita memproses orang tersebut yang kecepatannya lebih besar, jika kita mengikuti langkah-langkah di atas, kita akan tetap memperhitungkan orang ke-$i$, karena pada saat itu, orang ke-$i$ sudah diproses.
- Tandai orang ke-$i$ sebagai “sudah diproses”.
Maka, tiap kali kita memroses orang ke-$i$, kita perlu tahu banyaknya orang yang sudah diproses di dalam area berikut:
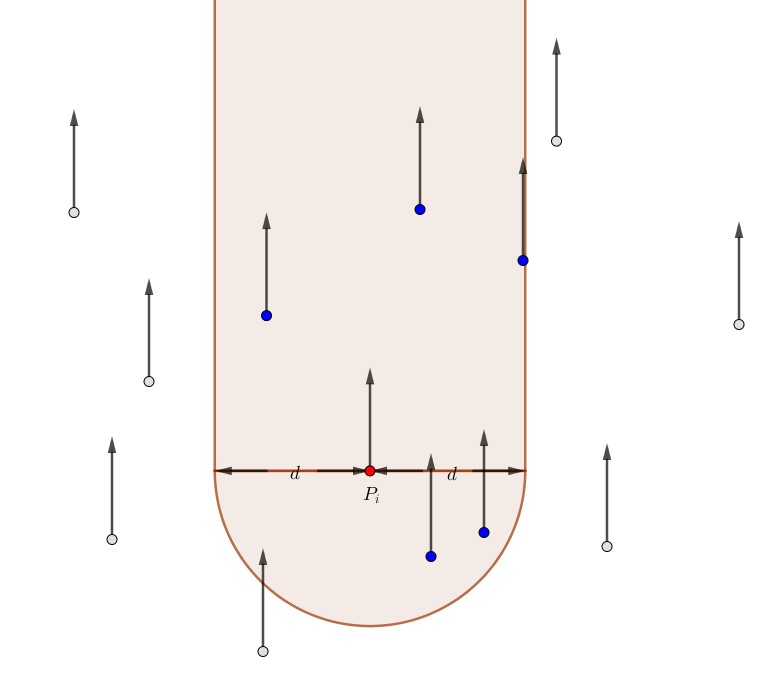
Perhatikan bahwa langkah-langkah di atas akan menghasilkan jawaban yang benar, hanya jika nilai $v_i$ berbeda-beda. Oleh karena itu, kita harus memproses orang-orang dengan nilai $v_i$ yang sama secara terpisah.
Saat nilai $v_i$ sama, maka yang terpenting hanyalah jarak antara keduanya. Berarti, kita harus dapat mencari banyaknya pasangan orang yang jaraknya kurang dari atau sama dengan $d$. Kita dapat melakukan hal yang serupa seperti di atas:
- Kumpulkan semua orang dengan nilai $v$ yang sama. Untuk orang-orang dengan nilai $v$ yang sama ini, kita akan proses satu per satu.
- Cari banyaknya orang (dengan nilai $v$ yang sama) yang telah diproses dan berjarak kurang dari atau sama dengan $d$.
- Tandai orang ini sebagai “sudah diproses”. Kita harus memisahkan proses ini secara terpisah dari proses sebelumnya (dan dari proses-proses dengan nilai $v$ yang berbeda).
2. Menghitung pasangan orang yang berlawanan arah
Pertama-tama, kita tandai semua orang dengan arah ke selatan ($v_i < 0$) sebagai sudah diproses. Kemudian, kita akan iterasi satu per satu orang dengan arah ke utara ($v_i \ge 0$). Misalkan kita akan memproses orang ke-$i$.
- Pada subkasus 2.1 di atas, orang ke-$i$ akan menabrak semua orang yang berlawanan arah dan posisi $y$ nya lebih utara.
- Pada subkasus 2.2 di atas, orang ke-$i$ akan menabrak semua orang yang berlawanan arah, posisi $y$ nya lebih rendah, dan jaraknya $\le d$.
Berarti, untuk tiap orang dengan $v_i \ge 0$, kita harus mencari banyaknya orang dengan $v_i < 0$ di dalam area berikut:
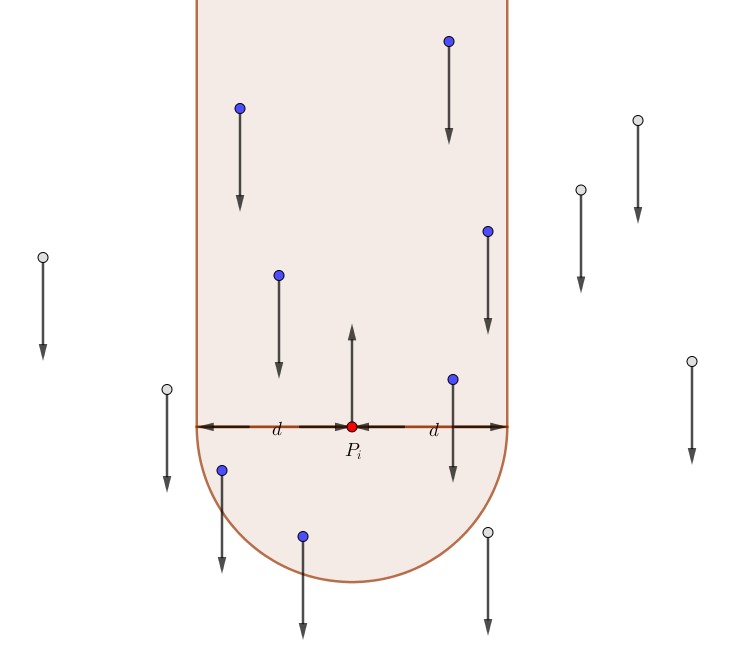
Hal ini (secara kebetulan) serupa dengan perhitungan pasangan orang yang berarah sama.
Struktur data yang dipakai
Sekarang yang tersisa adalah mencari suatu struktur data yang:
- Dapat meng-insert suatu titik $(x_i, y_i)$ ke dalam struktur data ini
- Dapat mencari banyaknya titik dalam area yang ditentukan seperti di atas
Kita dapat memanfaatkan fakta bahwa nilai $d$ hanya sampai 10, dan nilai $x$ yang hanya sampai 100 ribu. Berarti, kita dapat menyimpan informasi struktur data secara terpisah untuk setiap nilai $x$ yang berbeda. Lalu, untuk tiap query di atas, kita lakukan $2\times d + 1$ query terpisah untuk masing-masing nilai $x$.
Bentuk operasi di atas mirip dengan operasi pada Fenwick Tree / Binary Indexed Tree. Kita dapat memodifikasi BIT untuk menghasilkan struktur data yang kita inginkan.
Untuk tiap nilai $x$, kita simpan semua nilai $y$ yang “penting” (atau dengan kata lain yang ada titiknya pada masukan), kemudian urutkan nilai tersebut.
Kita dapat menggabungkan BIT dengan nilai $y$ yang terurut untuk membentuk struktur data sebagai berikut. Untuk tiap query, kita dapat mencari indeks nilai $y$ yang dicari dengan menggunakan binary search, kemudian lakukan query seperti biasa pada BIT yang kita punya.
Berikut adalah contoh pseudocode dari struktur data kita.
struct RangeBIT {
int n // banyaknya nilai y
int y[] // nilai y
BIT bit // kita menyimpan struktur BIT untuk melakukan operasi-operasi update & query
// inisiasi RangeBIT dengan nilai y tertentu
// nilai ini harus sudah terurut sebelumnya
constructor RangeBIT(int[] yvalues) {
n = size(yvalues)
y = yvalues
bit = new BIT(n) // kita harus memastikan ukuran BIT kita sesuai dengan banyaknya nilai y
}
// menambahkan nilai pada yadd sebesar value
// nilai yadd harus ada pada array y[] kita
function add(int yadd, int value) {
// cari index yadd pada array y kita dengan menggunakan binary search
int index = lowerBound(yadd, y)
// lakukan update pada BIT seperti biasa
bit.update(index, value)
}
// menghitung jumlah nilai di rentang [yl, yr]
function query(int yl, int yr) {
int indexl = lowerBound(yl, y)
int indexr = upperBound(yr, y) - 1
return bit.query(indexr) - bit.query(indexl-1)
}
}
Kompleksitas memori struktur data di atas adalah sejumlah banyaknya titik yang ada, jadi total kompleksitas memori adalah $O(N)$.
Sementara itu, kompleksitas waktu tiap query bisa mencapai $O(\log N)$, dan total ada $O(Nd)$ query. Sehingga total kompleksitas waktu adalah $O(Nd \log N)$.