Art Gallery
Kembali ke /editorial| Tingkat Kesulitan | Expert |
| Kategori | Computational Geometry |
| Pranala Soal | Pranala Soal |
| Pranala Solusi | Solusi Naif, Solusi Penuh |
Nilai 10%: menghitung luas poligon
Untuk mendapatkan 10% nilai pada soal ini, kita cukup menghitung luas poligon $G$. Kita bisa melakukannya bahkan dengan kurang dari 20 baris kode, dengan menggunakan determinan. Area dari poligon dengan titik-titik $(Gx_1, Gy_1)$, $(Gx_2, Gy_2)$, $\dots$, $(Gx_n, Gy_n)$ adalah:
\[\dfrac{1}{2}\left\lvert (Gx_1Gy_2 + Gx_2Gy_3 + \dots + Gx_nGy_1) - (Gy_1Gx_2 + Gy_2Gx_3 + \dots + Gy_nGx_1) \right\rvert\]
Berikut adalah implementasinya dalam bahasa C++:
#include <bits/stdc++.h>
using namespace std;
double x[5005], y[5005];
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++i) {
scanf("%lf%lf", &x[i], &y[i]);
}
double area = 0;
for (int i = 0; i < n; ++i) {
area += 0.5 * (x[i]*y[(i+1)%n] - x[(i+1)%n]*y[i]);
}
printf("%.17lf\n", area);
}Cara “Naif”
Sekarang untuk menyelesaikan soal yang sebenarnya, ada cara yang “naif” atau “straightforward”:
- Untuk setiap segmen, hitung area yang terkena cahaya pada segmen tersebut.
Perhatikan bahwa kita tidak perlu membedakan antara segmen lukisan dan segmen sisi poligon. Kita dapat menghitungnya dengan cara “memotong” setiap segmen dengan seluruh segmen lainnya, seperti yang diilustrasikan pada gambar berikut:
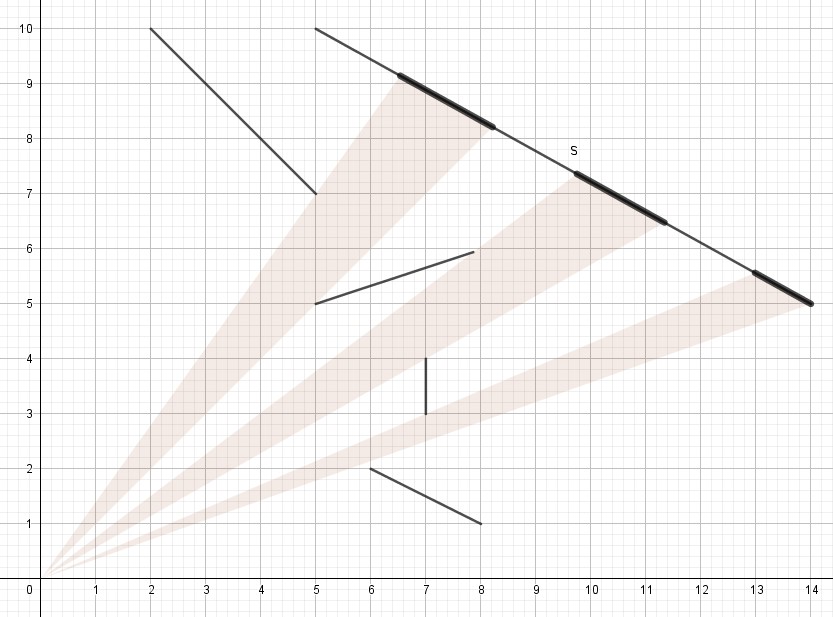
Langkah-langkahnya adalah sebagai berikut:
- Untuk setiap segmen (baik lukisan maupun sisi poligon), buat list segmen $S$ yang pada awalnya hanya berisi segmen tersebut.
- Untuk setiap segmen $t$ lainnya:
- Buat list segment temporer $Temp$ yang awalnya kosong.
- “Potong” setiap segment $s$ pada $S$ dengan segmen $t$. Misalkan $t$ memotong segmen $s$ menjadi segmen-segmen $s_1, s_2, \dots, s_k$, masukkan semuanya ke $Temp$.
- Assign $S = Temp$.
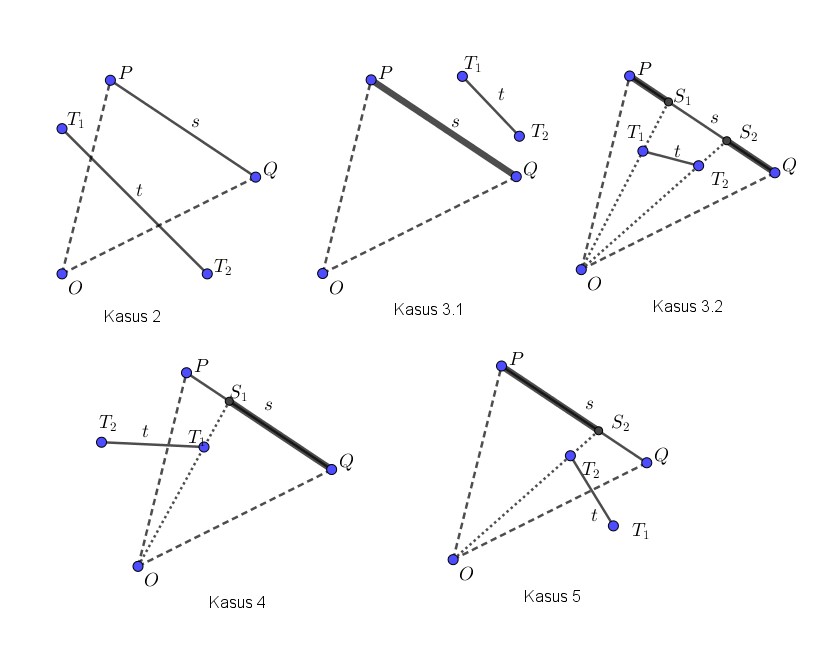
Sementara itu, berikut adalah kasus-kasus pemotongan sebuah segmen $s$ dengan segmen $t$ menjadi beberapa bagian:
- Misalkan segmen $s$ dibentuk dari titik-titik $P$ dan $Q$, dan $t$ dibentuk dari titik-titik $T_1$ dan $T_2$. Misalkan origin $(0,0)$ adalah $O$.
- Jika segmen $OP$ dan $OQ$ keduanya memotong $t$, maka segmen $s$ “tertutup sempurna” oleh $t$. Berarti hasil potongannya adalah 0 segmen.
- Jika segmen $OP$ dan $OQ$ keduanya tidak memotong $t$, maka:
- Cek salah satu titik pada $t$, apakah dia berada di dalam segitiga $OPQ$. Jika tidak, maka segmen $s$ tidak terpotong oleh $t$. Berarti hasil potongannya adalah segmen $s$ semula.
- Jika di dalam, maka segmen $t$ memotong $s$ menjadi dua bagian. Cari perpotongan $OT_1$ dan $OT_2$ dengan $s$, misalkan $S_1$ dan $S_2$. Hasil potongannya adalah $PS_1$ dan $QS_2$, jika $P$ lebih dekat ke $S_1$ dibandingkan $S_2$. Jika tidak, maka hasil potongannya adalah $PS_2$ dan $QS_1$.
- Jika segmen $OP$ memotong $t$:
- Berarti salah satu titik pada $t$ berada di dalam segitiga $OPQ$. Misalkan $T_1$ berada di dalam segitiga $OPQ$, dan $OT_1$ memotong $s$ di $S_1$. Berarti, hasil potongannya adalah satu segmen $QS_1$.
- Jika segmen $OQ$ yang memotong $t$, lakukan cara yang sama dengan nomor 4.
Kompleksitas
Kasus terburuknya adalah tiap segmen dapat terbagi menjadi $(M+N)$ segmen. Dan ke-$M$ segmen ini harus “dipotong” dengan $(M+N)$ segmen lainnya. Jadi, kompleksitasnya bisa mencapai $O((M+N)^3)$, walaupun pada sebagian besar kasus, kompleksitasnya lebih mendekati kuadratik.
Solusi ini akan mendapatkan nilai sekitar 70-80% pada kasus uji yang ada.
Nilai 100%: Solusi $O(M^2)$
Kita dapat mengembangkan solusi “memotong segmen” di atas dengan cara terlebih dahulu mengurutkan tiap segmen berdasarkan sudutnya. Kita urutkan semua segmen berdasarkan sudut yang dibentuk antara sumbu $x$ dengan segmen $OP$ di mana $P$ dan $Q$ adalah titik-titik pembentuk segmen, dan $P$ adalah titik dengan sudut terkecil.
Untuk seterusnya, kita akan sebut sudut $xOP$ sebagai sudut pertama dari segmen $PQ$, dan sudut $xOQ$ sebagai sudut kedua dari segmen $PQ$. Berarti, kita terlebih dulu mengurutkan segmen-segmen berdasarkan sudut pertamanya.
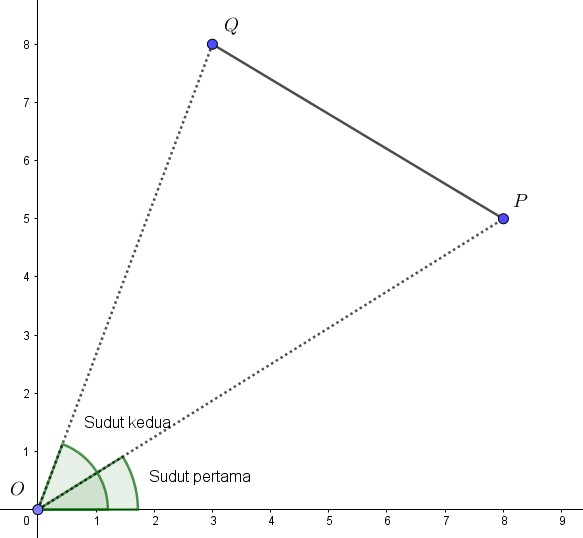
Untuk dapat mengurutkan dengan benar, sebelumnya kita harus membagi dua seluruh segmen yang berpotongan dengan sumbu $x$ positif.
Pertama-tama, kita maintain sebuah list segmen $S$ yang berisi segmen-segmen yang “sedang diproses”. Awalnya $S$ kosong. Nantinya dapat dibuktikan bahwa segmen-segmen di $S$ akan selalu berbentuk seperti berikut:
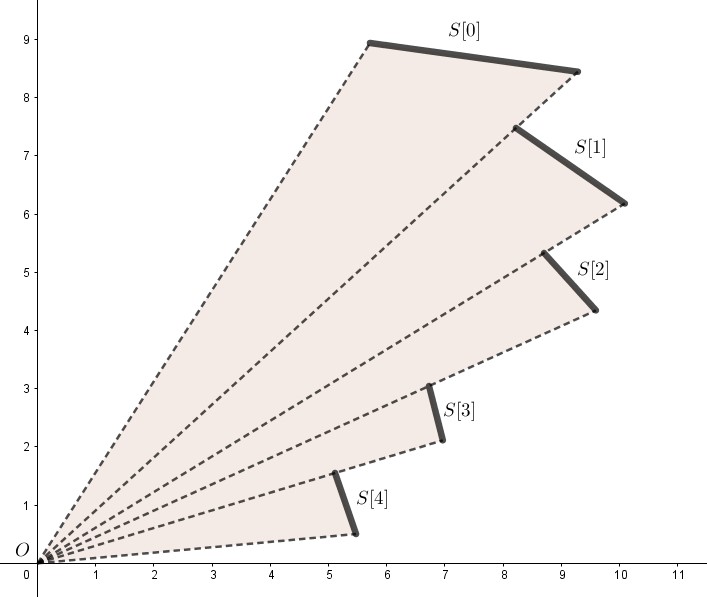
Atau dengan kata lain, sudut pertama $S[0]$ sama dengan sudut kedua $S[1]$, sudut pertama $S[1]$ sama dengan sudut kedua $S[2]$, dst.
Selain itu, kita juga perlu menyimpan list segmen lain, $Ans$, yang berisi segmen final yang tidak akan terpotong oleh segmen lainnya lagi.
Untuk tiap segmen $s$ pada masukan (yang telah terurut berdasarkan sudut pertama), kita lakukan langkah-langkah berikut:
-
Untuk semua segmen pada $S$ yang sudut keduanya kurang dari sudut pertama $s$, hapus dari $S$ dan masukkan ke $Ans$. Kita mengurutkan segmen pada $S$ menurun berdasarkan sudutnya, jadi yang kita lakukan sama saja dengan menghapus elemen-elemen terakhir $S$ selama sudut keduanya kurang dari sudut pertama $s$.
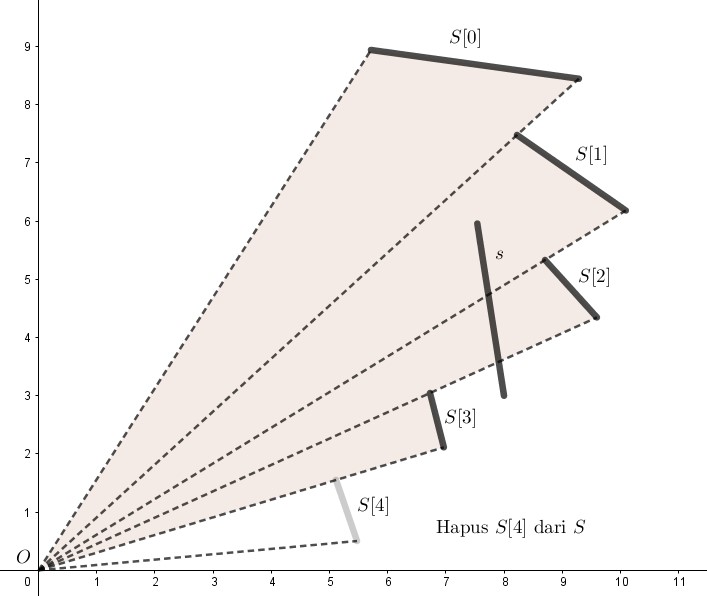
-
“Potong” segmen terakhir pada $S$ sehingga sudut pertamanya sama dengan sudut pertama $s$. Hasil potongannya ini kita masukkan ke dalam $Ans$.
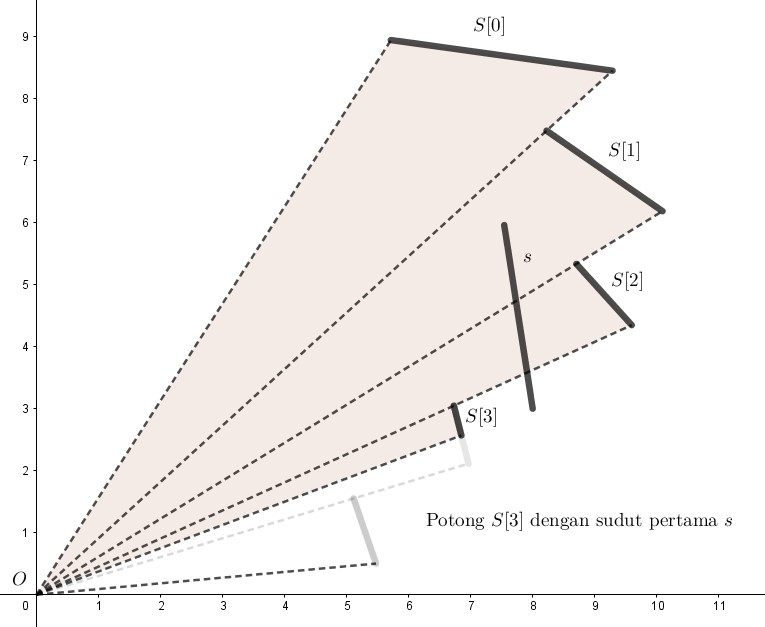
Alasan kita melakukan hal ini adalah karena semua segmen terurut berdasarkan sudut pertama, berarti kita tidak akan menemukan segmen dengan sudut yang kurang dari ini. Berarti kita bisa yakin bahwa hasil potongannya pasti masuk ke $Ans$.
-
Misalkan $k$ adalah indeks terakhir $S$ (atau $k = size(S) - 1$ jika kita menggunakan indeks 0). Kurangi $k$ sampai $s$ “berada di depan” $S[k]$. Secara formal, $s$ berada di depan $S[k]$ jika $s$ memotong segmen $OS[k]_1$, di mana $S[k] = S[k]_1S[k]_2$.
Pada contoh di atas, berarti $k = 2$.
Jika $s$ “berada di belakang” seluruh segmen pada $S$, maka kita langsung berhenti memproses $s$ dan dapat langsung melanjutkan ke segmen berikutnya pada masukan.
-
Set variable lain $rk = k$, dan kurangi $rk$ sampai $rk$ adalah indeks terkecil sehingga $s$ masih berada di depan $S[rk]$. Berarti, $S[rk-1]$ sudah tidak tertutup oleh $s$.
Pada contoh di atas, berarti $rk = 1$.
-
Seperti yang ditunjukkan pada diagram di atas, berarti seluruh segmen dari $S[rk+1]$ hingga $S[k]$ akan tertutup oleh $s$. Maka, hapus semuanya dari $S$ dan jangan masukkan ke $Ans$, karena segmen-segmen tersebut “tidak terlihat” lagi.
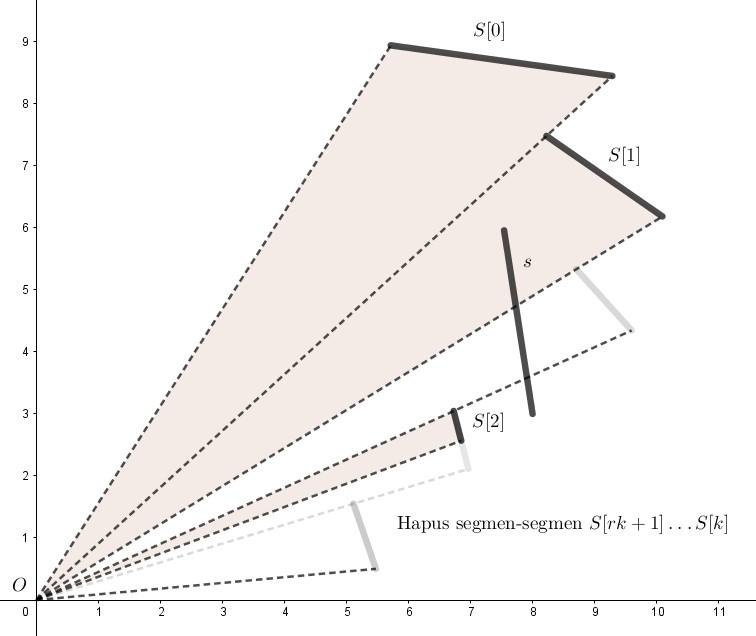
-
Perhatikan bahwa khusus untuk segmen $S[rk]$, ada kemungkinan bahwa dia akan terpotong menjadi dua. Hapus bagian yang “tertutup” oleh $s$, dan ubah $S[rk]$ menjadi bagian yang “masih terlihat”.
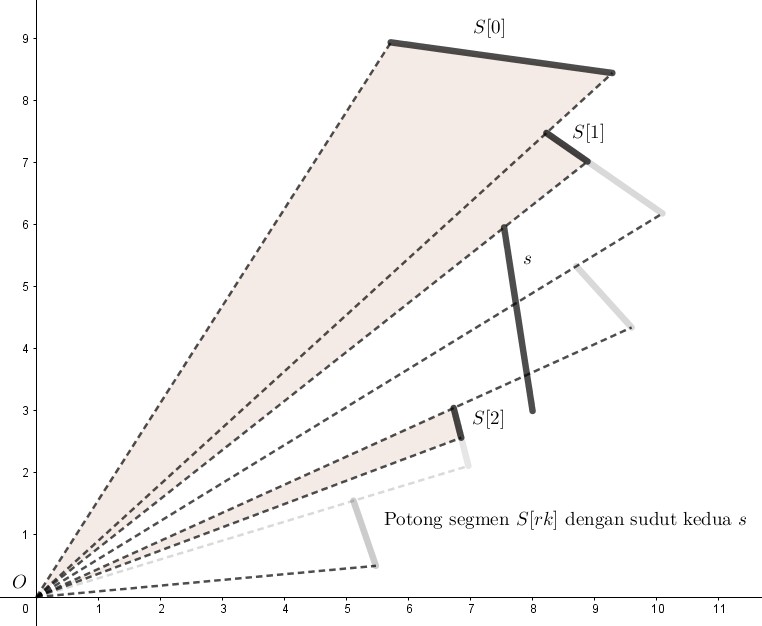
-
Masukkan $s$ yang “masih terlihat” ke dalam list $S$ pada indeks setelah $S[rk]$.
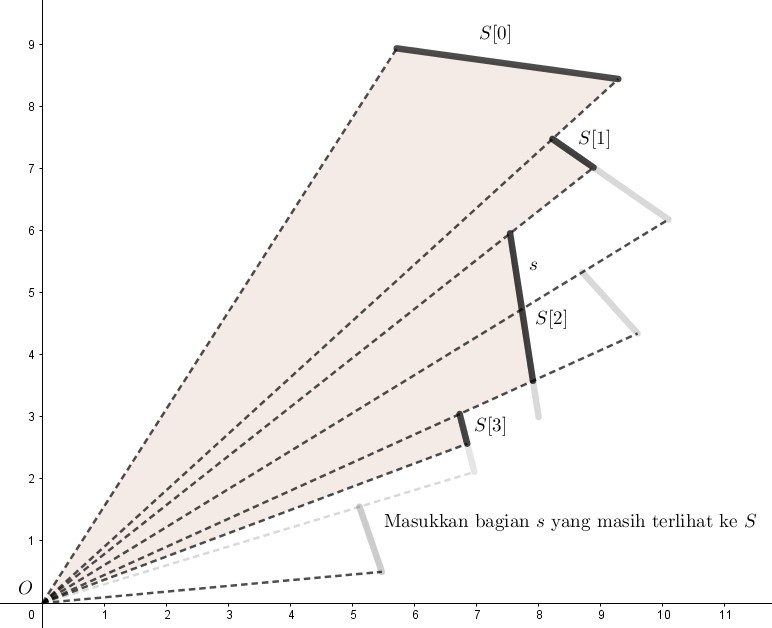
Kita ulangi langkah-langkah di atas hingga semua segmen diproses.
Setelah semua segmen diproses, kita juga harus memasukkan semua segmen yang tersisa di $S$ ke $Ans$. Jawabannya adalah total area segitiga yang dibentuk antara $O$ dan kedua titik segmen-segmen pada $Ans$.
Kompleksitas
Karena tiap kali kita memroses sebuah segmen, paling banyak ada satu operasi insert, maka paling banyak ada $O(M+N)$ segmen yang ada pada $S$. Dan pada tiap kali kita memroses sebuah segmen, kita bisa melakukan iterasi sebanyak $size(S)$. Jadi, kompleksitas terburuknya adalah $O((M+N)^2)$. Namun, perhatikan bahwa paling banyak hanya ada satu sisi poligon yang ada di dalam $S$. Jadi, kompleksitasnya tidak akan lebih buruk dari $O(M^2)$.
Lebih jauh lagi: solusi $O(M \log^2 M)$
Solusi di atas lebih dari cukup untuk mendapatkan nilai penuh. Implementasi juri membutuhkan waktu kurang dari 0.2s pada semua kasus saat dijalankan di platform Hackerrank.
Namun, kita dapat mengambil langkah lebih jauh lagi untuk mendapatkan solusi $O(M \log^2 M)$, dengan cara menggunakan struktur data selain list untuk menyimpan $S$.
Perhatikan bahwa $S$ memerlukan properti-properti berikut:
- Segmen-segmen pada $S$ terurut berdasarkan sudut pertamanya
- Kita dapat menghapus segmen pada $S$, baik di ujung maupun di tengah-tengah
- Kita harus dapat mencari indeks $k$ dan $rk$ seperti yang dijelaskan pada bagian sebelumnya
- Kita dapat meng-insert segmen pada $S$ di tengah-tengah
Kita dapat menggunakan balanced binary search tree seperti AVL Tree sebagai struktur data untuk menyimpan segmen-segmen pada $S$. Perhatikan bahwa elemen-elemen pada AVL Tree sudah otomatis terurut, dan kita dapat melakukan operasi insertion dan deletion dalam $O(\log N)$ di mana $N$ adalah banyak elemen pada tree.
Yang tersisa adalah properti 3, yaitu bagaimana cara mencari indeks $k$ dan $rk$. Perhatikan bahwa properti urutan segmen pada $S$ membuat kita bisa melakukan binary search untuk mencari $r$ dan $rk$. Dan kita dapat mengakses elemen ke-$i$ pada AVL Tree dalam $O(\log N)$, sehingga kita bisa mencari nilai $r$ dan $rk$ dalam $O(\log^2 M)$.
Jadi tiap segmen dapat diproses dalam $O(\log^2 M)$ sehingga kompleksitas totalnya adalah $O(M \log^2 M)$. Implementasinya sendiri diserahkan kepada pembaca sebagai latihan.
Apendiks: Perhitungan geometri
Salah satu hal yang membuat soal ini sulit adalah karena sulitnya mengimplementasikan operasi-operasi dalam computational geometry. Bahkan untuk mendapatkan nilai 30% dalam soal ini, tetap diperlukan algoritma dengan kompleksitas $O(M^2)$ seperti di atas, tapi karena seluruh segmen yang sejajar dengan sumbu x, maka operasi-operasi geometrinya jadi jauh lebih sederhana.
Berikut adalah operasi-operasi yang dibutuhkan dalam menyelesaikan soal ini beserta implementasinya.
Struktur Data Point dan Segment
Struktur data yang dipakai cukup straightforward. Kita menggunakan pair dua buah double untuk point dan menggunakan pair dua buah point untuk segment.
struct point{
double x, y;
point() { x = y = 0; }
point(double x, double y) : x(x), y(y) {}
};
struct segment {
point p1, p2;
segment() {p1 = p2 = point(0,0);}
segment(point p1, point p2) : p1(p1), p2(p2) {}
};Mencari perpotongan dua garis
Garis berbeda dengan segmen. Segmen terbatas di kedua titik ujungnya, sementara garis dapat diperpanjang sampai tak hingga.
Berikut adalah cara menghitung perpotongan dua garis, mengikuti rumus yang diberikan pada Wikipedia:
point intersection(const segment &s1, const segment &s2){
/* assumes !isParallel(s1,s2) */
double x1 = s1.p1.x - s1.p2.x;
double x2 = s2.p1.x - s2.p2.x;
double y1 = s1.p1.y - s1.p2.y;
double y2 = s2.p1.y - s2.p2.y;
double cross1 = cross(s1.p1, s1.p2);
double cross2 = cross(s2.p1, s2.p2);
return point ((cross1 * x2 - cross2 * x1) / (x1 * y2 - x2 * y1), (cross1 * y2 - cross2 * y1) / (x1 * y2 - x2 * y1));
}Di mana cross adalah cross product.
double cross(const point &p1, const point &p2) {
return p1.x * p2.y - p1.y * p2.x;
}Menentukan apakah suatu titik ada pada segmen
Ada penjelasan yang bagus di Stackoverflow tentang cara menentukan apakah suatu titik ada pada segmen atau tidak.
bool isOnSegment(const point &p, const segment &s){
double c = cross(p - s.p1, s.p2 - p);
if (fabs(c) > EPS) return false;
double d = dot(s.p2 - s.p1, p - s.p1);
return d > -EPS && d < sqr(s.p2.x - s.p1.x) + sqr(s.p2.y - s.p1.y) + EPS;
}Di mana dot adalah dot product antara dua titik.
double dot(const point &p1, const point &p2) {
return p1.x * p2.x + p1.y * p2.y;
}Menentukan apakah dua segmen berpotongan
Kita dapat mencari perpotongan dua garis tersebut dan mengecek apakah titik tersebut ada pada kedua segmen.
Ada cara lain untuk menentukan apakah dua segmen berpotongan. Misalkan $s_1 = PQ$ dan $s_2 = ST$. Kedua segmen $s_1$ dan $s_2$ akan berpotongan jika:
- $P$ dan $Q$ ada di sisi yang berbeda terhadap garis $ST$, dan
- $S$ dan $T$ ada di sisi yang berbeda terhadap garis $PQ$.
Kita dapat memeriksa apakah dua titik ada di sisi yang sama atau tidak terhadap sebuah garis dengan menggunakan metode berikut:
bool isOnSameSide(const point &p1, const point &p2, const segment &s){
double z1 = cross(s.p2 - s.p1, p1 - s.p1);
double z2 = cross(s.p2 - s.p1, p2 - s.p1);
return (z1 + EPS < 0 && z2 + EPS < 0) || (0 < z1 - EPS && 0 < z2 - EPS) || fabs(z1) < EPS || fabs(z2) < EPS;
/* on segment returns true */
}Selain itu, kita juga perlu memeriksa apakah $P$ atau $Q$ ada di segmen $ST$ atau sebaliknya, $S$ atau $T$ ada di segmen $PQ$.
bool isIntersecting(const segment &s1, const segment &s2){
return !(isOnSameSide(s1.p1,s1.p2,s2) || isOnSameSide(s2.p1,s2.p2,s1))
|| isOnSegment(s1.p1,s2) || isOnSegment(s1.p2,s2)
|| isOnSegment(s2.p1,s1) || isOnSegment(s2.p2,s1);
}Menentukan apakah titik ada di dalam poligon atau tidak
Kita dapat menentukan titik ada di dalma poligon atau tidak dengan menggunakan metode Ray Casting.
Namun, jika poligon yang dicari adalah segitiga (seperti pada soal ini), maka ada cara yang lebih mudah, yaitu dengan membandingkan centroid $G = (A + B + C) / 3$ dengan titik tersebut. Centroid pasti ada di dalam suatu segitiga. Jadi suatu titik ada di dalam segitiga jika dan hanya jika dia berada di sisi yang sama dengan $G$ terhadap ketiga sisi segitiga.
Operasi-operasi lainnya
Masih banyak operasi dalam computational geometry, tapi operasi-operasi di atas cukup untuk menyelesaikan soal ini.
Kalian dapat melihat library Geometri yang digunakan juri di sini. Contohnya ada beberapa fungsi seperti algoritma Ray-casting di atas, dan Convex Hull, yang dibutuhkan untuk meng-generate kasus uji.
Apendiks 2: Visualisasi beberapa kasus uji
Sebagai bonus, berikut adalah visualisasi beberapa kasus yang diikutsertakan. Visualisasi dilakukan oleh Geogebra. Karena alasan limitasi Geogebra, kasus-kasus yang dipilih adalah kasus-kasus dengan nilai $N$ dan $M$ yang kecil (100 atau kurang).
Inverse Pyramid
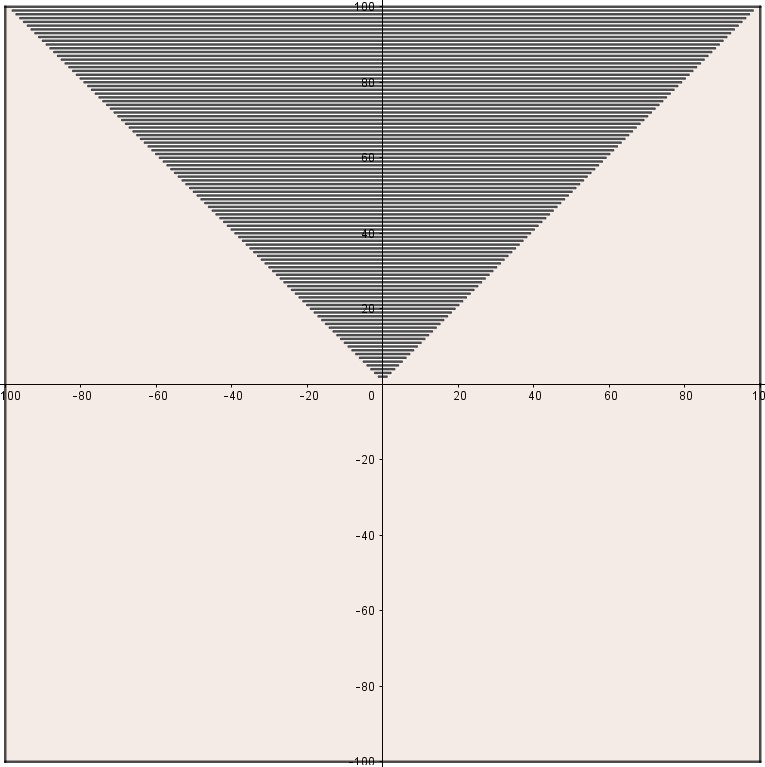
Jika diperbesar, dapat terlihat bahwa semua segmen pada kasus ini terkena cahaya di ujungnya walaupun sangat sedikit.
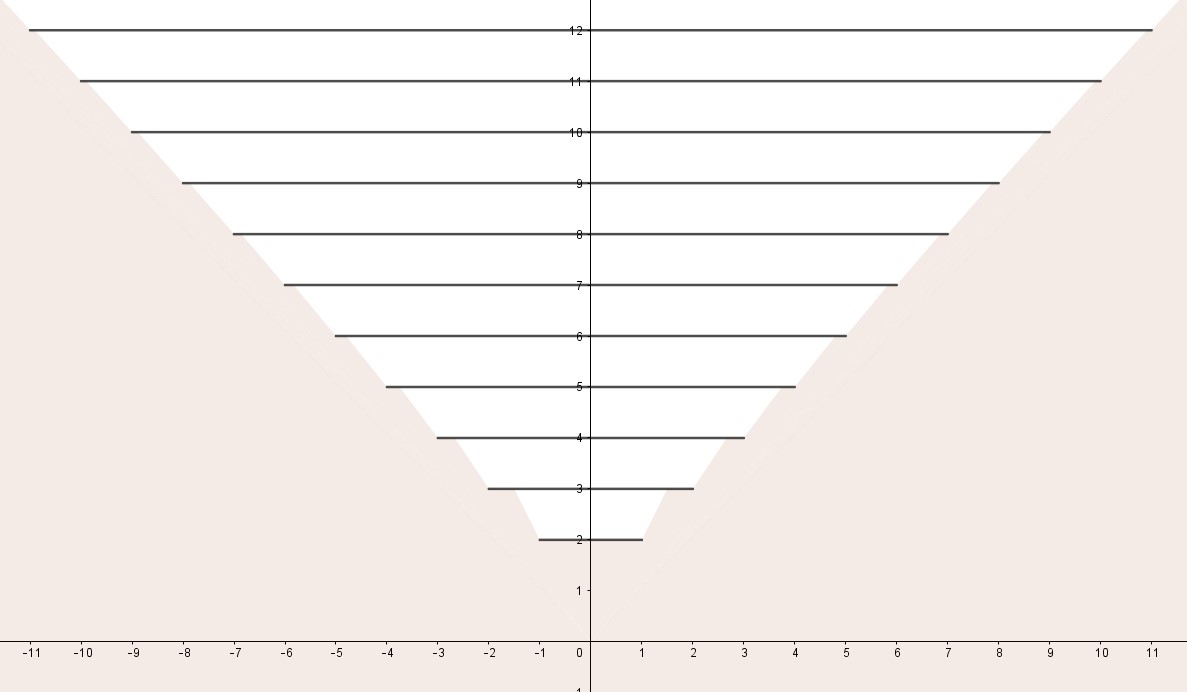
Windmill
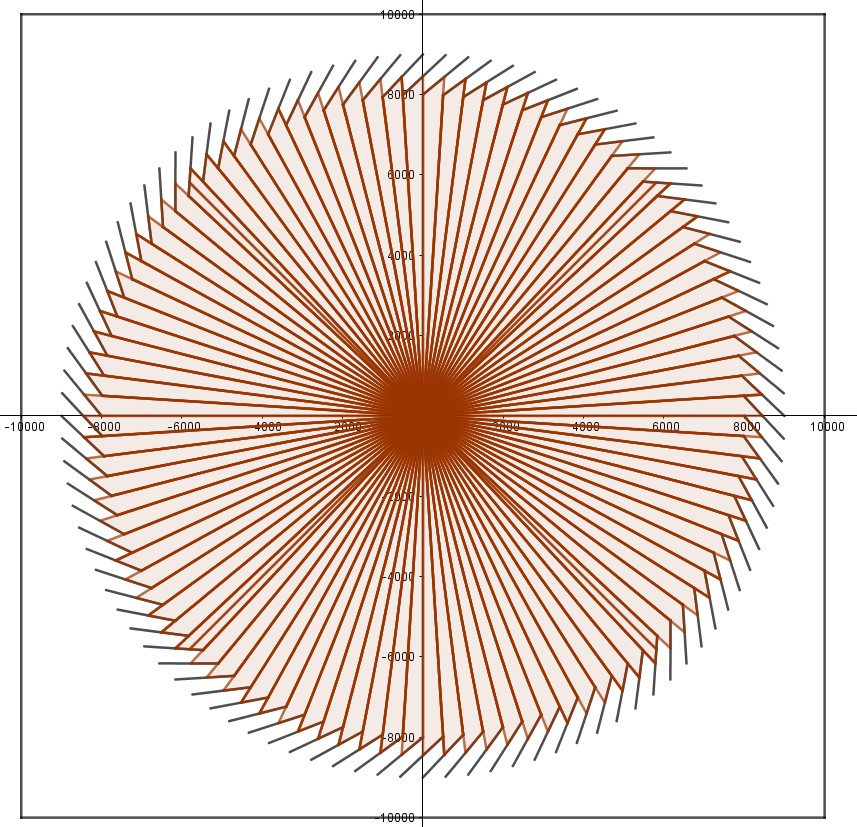
Random
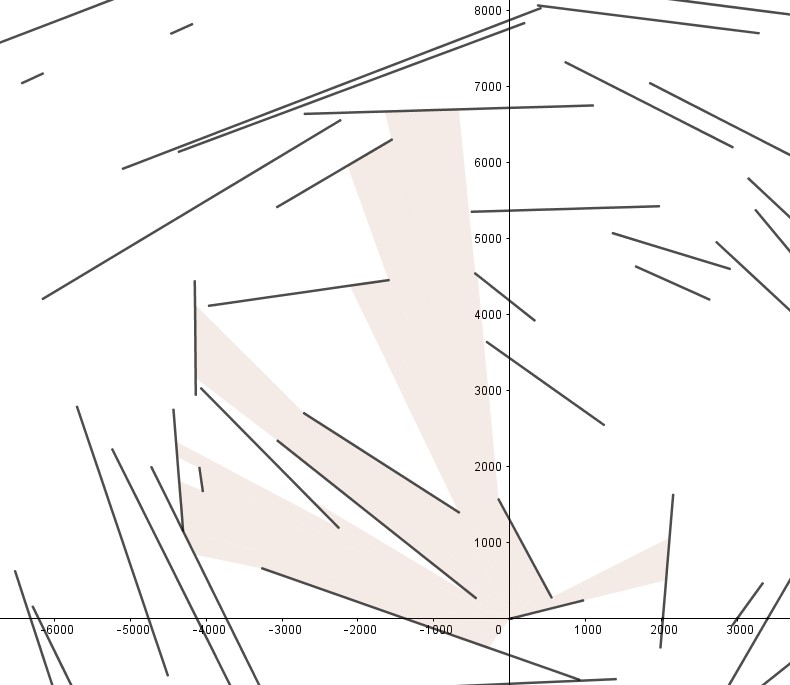
Ini menunjukkan bahwa jika kita meng-generate banyak segmen random, kemungkinan besar yang terkena cahaya hanya sebagian kecil segmen yang berada di dekat $(0, 0)$.